Référence du fichier float.h

paramètres décrivant les types flottants Plus de détails...

Macros

#define FLT_RADIX
 base
#define FLT_MANT_DIG
 résolution des float
#define DBL_MANT_DIG
 résolution des double
#define LDBL_MANT_DIG
 résolution des long double
#define FLT_DIG
 résolution décimale des float
#define DBL_DIG
 résolution décimale des double
#define LDBL_DIG
 résolution décimale des long double
#define FLT_MIN_EXP
 exposant minimal des float
#define DBL_MIN_EXP
 exposant minimal des double
#define LDBL_MIN_EXP
 exposant minimal des long double
#define FLT_MIN_10_EXP
 exposant de 10 minimal des float
#define DBL_MIN_10_EXP
 exposant de 10 minimal des double
#define LDBL_MIN_10_EXP
 exposant de 10 minimal des long double
#define FLT_MAX_EXP
 exposant maximal des float
#define DBL_MAX_EXP
 exposant maximal des double
#define LDBL_MAX_EXP
 exposant maximal des long double
#define FLT_MAX_10_EXP
 exposant de 10 maximal des float
#define DBL_MAX_10_EXP
 exposant de 10 maximal des double
#define LDBL_MAX_10_EXP
 exposant de 10 maximal des long double
#define FLT_MAX
 valeur maximale des float
#define DBL_MAX
 valeur maximale des double
#define LDBL_MAX
 valeur maximale des long double
#define FLT_EPSILON
 epsilon des float
#define DBL_EPSILON
 epsilon des double
#define LDBL_EPSILON
 epsilon des long double
#define FLT_MIN
 valeur minimale des float
#define DBL_MIN
 valeur minimale des double
#define LDBL_MIN
 valeur minimale des long double

Description détaillée

Cet entête fournit des macros donnant divers paramètres décrivant les types flottants.

Les flottants sont des nombres de la forme:

\[\pm i\;r^{e-p}\]

avec

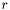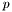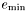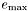Les différents paramètres donnés dans cet entête sont déduisibles de $r$, $p$, $e_{\mbox{\scriptsize min}}$ et $e_{\mbox{\scriptsize max}}$.

Les nombres en virgule flottante donne plus d'informations sur la représentation en virgule flottante.

Documentation des macros

#define DBL_DIG

\[ \left\{\begin{array}{ll} p \; \log_{10} r & \mbox{si $r$ est une puissance de 10} \\ \lfloor (p-1)\;\log_{10} r\rfloor & \mbox{sinon} \end{array}\right. \]

Le nombre de chiffres en base 10 que le format double est capable de représenter.

Note:

La norme C90 contient une erreur dans la formule dans le cas où la base est une puissance de 10, elle est corrigée ici.

#define DBL_EPSILON

$b^{1-p}$

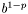
Différence la plus petite valeur représentable comme un double plus grande que 1 et 1.

Note:
On trouve parfois donnée comme définition la plus petite valeur 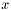$x$ telle que 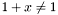$1+x \ne 1$; cette définition a le problème de pouvoir être deux fois plus petite que la valeur réelle à cause des arrondis.
#define DBL_MANT_DIG

$p$

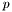
Le nombre de chiffres en base 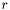$r$ que le format double est capable de représenter.

#define DBL_MAX

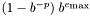
$(1-b^{-p})\;b^{e_{\mbox{\scriptsize max}}}$

Valeur maximale finie représentable comme un double.

#define DBL_MAX_10_EXP

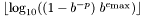
$\lfloor \log_{10}((1-b^{-p}) \; b^{e_{\mbox{\scriptsize max}}}) \rfloor$

La puissance maximale de 10 représentable de manière finie comme un double.

#define DBL_MAX_EXP

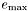
$e_{\mbox{\scriptsize max}}$

Un de plus que la puissance maximale de 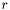$r$ représentable de manière finie comme un double.

#define DBL_MIN

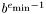
$b^{e_{\mbox{\scriptsize min}}-1}$

La valeur minimale représentable de manière normalisée comme un double.

#define DBL_MIN_10_EXP

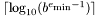
$\lceil \log_{10}(b^{e_{\mbox{\scriptsize min}}-1}) \rceil$

La puissance minimale de 10 représentable de manière normalisée comme un double.

#define DBL_MIN_EXP

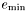
$e_{\mbox{\scriptsize min}}$

Un de plus que la puissance minimale de 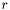$r$ représentable de manière normalisée comme un double.

#define FLT_DIG

\[ \left\{\begin{array}{ll} p \; \log_{10} r & \mbox{si $r$ est une puissance de 10} \\ \lfloor (p-1)\;\log_{10} r\rfloor & \mbox{sinon} \end{array}\right. \]

Le nombre de chiffres en base 10 que le format float est capable de représenter.

Note:

La norme C90 contient une erreur dans la formule dans le cas où la base est une puissance de 10, elle est corrigée ici.

#define FLT_EPSILON

$b^{1-p}$

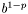
Différence la plus petite valeur représentable comme un float plus grande que 1 et 1.

Note:
On trouve parfois donnée comme définition la plus petite valeur 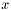$x$ telle que 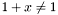$1+x \ne 1$; cette définition a le problème de pouvoir être deux fois plus petite que la valeur réelle à cause des arrondis.
#define FLT_MANT_DIG

$p$

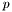
Le nombre de chiffres en base 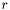$r$ que le format float est capable de représenter.

#define FLT_MAX

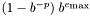
$(1-b^{-p})\;b^{e_{\mbox{\scriptsize max}}}$

Valeur maximale finie représentable comme un float.

#define FLT_MAX_10_EXP

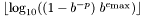
$\lfloor \log_{10}((1-b^{-p}) \; b^{e_{\mbox{\scriptsize max}}}) \rfloor$

La puissance maximale de 10 représentable de manière finie comme un float.

#define FLT_MAX_EXP

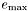
$e_{\mbox{\scriptsize max}}$

Un de plus que la puissance maximale de 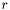$r$ représentable de manière finie comme un float.

#define FLT_MIN

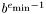
$b^{e_{\mbox{\scriptsize min}}-1}$

La valeur minimale représentable de manière normalisée comme un float.

#define FLT_MIN_10_EXP

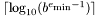
$\lceil \log_{10}(b^{e_{\mbox{\scriptsize min}}-1}) \rceil$

La puissance minimale de 10 représentable de manière normalisée comme un float.

#define FLT_MIN_EXP

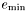
$e_{\mbox{\scriptsize min}}$

Un de plus que la puissance minimale de 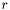$r$ représentable de manière normalisée comme un float.

#define FLT_RADIX

$r$

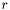
Les formats flottants doivent tous utiliser la même base, FLT_RADIX en donne la valeur.

#define LDBL_DIG

\[ \left\{\begin{array}{ll} p \; \log_{10} r & \mbox{si $r$ est une puissance de 10} \\ \lfloor (p-1)\;\log_{10} r\rfloor & \mbox{sinon} \end{array}\right. \]

Le nombre de chiffres en base 10 que le format long double est capable de représenter.

Note:

La norme C90 contient une erreur dans la formule dans le cas où la base est une puissance de 10, elle est corrigée ici.

#define LDBL_EPSILON

$b^{1-p}$

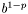
Différence la plus petite valeur représentable comme un long double plus grande que 1 et 1.

Note:
On trouve parfois donnée comme définition la plus petite valeur 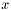$x$ telle que 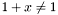$1+x \ne 1$; cette définition a le problème de pouvoir être deux fois plus petite que la valeur réelle à cause des arrondis.
#define LDBL_MANT_DIG

$p$

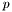
Le nombre de chiffres en base 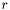$r$ que le format long double est capable de représenter.

#define LDBL_MAX

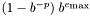
$(1-b^{-p})\;b^{e_{\mbox{\scriptsize max}}}$

Valeur maximale finie représentable comme un long double.

#define LDBL_MAX_10_EXP

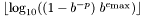
$\lfloor \log_{10}((1-b^{-p}) \; b^{e_{\mbox{\scriptsize max}}}) \rfloor$

La puissance maximale de 10 représentable de manière finie comme un long double.

#define LDBL_MAX_EXP

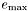
$e_{\mbox{\scriptsize max}}$

Un de plus que la puissance maximale de 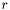$r$ représentable de manière finie comme un long double.

#define LDBL_MIN

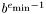
$b^{e_{\mbox{\scriptsize min}}-1}$

La valeur minimale représentable de manière normalisée comme un long double.

#define LDBL_MIN_10_EXP

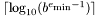
$\lceil \log_{10}(b^{e_{\mbox{\scriptsize min}}-1}) \rceil$

La puissance minimale de 10 représentable de manière normalisée comme un long double.

#define LDBL_MIN_EXP

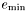
$e_{\mbox{\scriptsize min}}$

Un de plus que la puissance minimale de 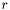$r$ représentable de manière normalisée comme un long double.

Copyright © 2008 -- 2009 Jean-Marc Bourguet Accueil Pages sur le C