Les nombres en virgule flottante
Introduction
Plusieurs techniques sont utilisées pour modéliser les réels, chacune avec des avantages et des inconvénients. La technique la plus répandue, c'est la représentation en virgule flottante; on appelle souvent les nombres représentables ou représentés dans une telle représentation des nombres flottants ou même simplement des flottants.Les nombres représentables en virgule flottante sont les rationnels exprimables sous la forme
![\[x = \pm i\;r^{e-p}\]](form_2.png)
où le signe, 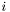 et
et 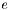 caractérisent le nombre:
caractérisent le nombre:
- la valeur
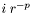 est appelée la partie fractionnaire du nombre, la valeur
est appelée la partie fractionnaire du nombre, la valeur 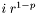 la partie significative de celui-ci. Ces définitions ne sont pas universellement employées; ces termes, de même que le terme de mantisse, sont souvent aussi utilisés pour désigner
la partie significative de celui-ci. Ces définitions ne sont pas universellement employées; ces termes, de même que le terme de mantisse, sont souvent aussi utilisés pour désigner 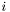 multiplié par une puissance fixée de
multiplié par une puissance fixée de 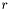 ; on a
; on a 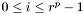 ;
;
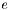 est l'exposant du nombre; on a
est l'exposant du nombre; on a 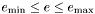 .
.
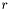 ,
, 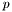 ,
, 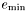 et
et 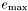 caractérisent le format:
caractérisent le format:
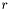 est la base de la représentation; la base de loin la plus courante est 2, certains tentent de repopulariser la base 10 et les bases 8 et 16 ont déjà été utilisées
est la base de la représentation; la base de loin la plus courante est 2, certains tentent de repopulariser la base 10 et les bases 8 et 16 ont déjà été utilisées
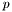 est la résolution de la représentation, le nombre de chiffres de base
est la résolution de la représentation, le nombre de chiffres de base 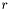 que le format est capable de représenter
que le format est capable de représenter
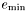 est la valeur minimale pour l'exposant
est la valeur minimale pour l'exposant
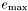 est la valeur maximale pour l'exposant
est la valeur maximale pour l'exposant
En plus de ces nombres, certains formats flottants peuvent représenter d'autres valeurs:
- un zéro négatif, dont l'utilité principale est dans l'analyse de fonctions complexes;
- des valeurs infinies
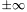 ;
;
- des NaN (Not a Number) utilisés pour indiquer qu'il n'y a pas de nombre.
On remarque que certains nombres flottants peuvent avoir plusieurs représentations, par exemple dans un format où 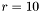 et
et 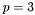 le nombre cent a pour représentations possibles
le nombre cent a pour représentations possibles 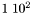 ,
, 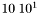 et
et 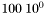 . Une représentation pour laquelle
. Une représentation pour laquelle 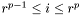 est appelée représentation normalisée.
est appelée représentation normalisée.
Les nombres 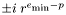 avec
avec 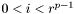 , qui donc n'ont pas de représentation normalisée, sont appelés nombre dénormaux ou sous-normaux. Certains formats de flottants n'autorisent pas les nombres dénormaux. En l'absence de dénormaux, la différence entre
, qui donc n'ont pas de représentation normalisée, sont appelés nombre dénormaux ou sous-normaux. Certains formats de flottants n'autorisent pas les nombres dénormaux. En l'absence de dénormaux, la différence entre 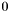 et plus petit nombre positif représentable est de
et plus petit nombre positif représentable est de 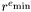 tandis que celle entre ce nombre et le suivant est de
tandis que celle entre ce nombre et le suivant est de 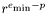 , soit une valeur beaucoup plus petite, ce qui peut poser des problèmes. En présence de dénormaux, la différence entre deux nombres dénormaux successifs est toujours de
, soit une valeur beaucoup plus petite, ce qui peut poser des problèmes. En présence de dénormaux, la différence entre deux nombres dénormaux successifs est toujours de 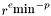 . La différence entre deux nombres ayant une représentation normalisée varie.
. La différence entre deux nombres ayant une représentation normalisée varie.
- Note:
- J'ai essayé ici de suivre les termes et les définitions utilisés par la norme LIA-1 (dans une traduction assez littérale) mais l'usage est loin d'être universel en particulier pour les termes désignants
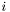 . Mantisse me semble être le terme le plus employé, mais sa définition varie beaucoup aussi.
. Mantisse me semble être le terme le plus employé, mais sa définition varie beaucoup aussi.En passant, depuis bien avant l'usage de représentations en virgule flottante, on utilise les termes de partie fractionnaire ou de mantisse pour
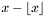 . Le terme de mantisse était en particulier utilisé dans le cadre des tables de logarithmes, où la partie entière d'un logarithme est appelé caractéristique. Cette note historique est l'occasion de faire remarquer qu'on peut considérer la représentation en virgule flottante d'un nombre comme une approximation de son logarithme -- l'exposant est la caractéristique du logarithme et la partie significative est proche de sa mantisse.
. Le terme de mantisse était en particulier utilisé dans le cadre des tables de logarithmes, où la partie entière d'un logarithme est appelé caractéristique. Cette note historique est l'occasion de faire remarquer qu'on peut considérer la représentation en virgule flottante d'un nombre comme une approximation de son logarithme -- l'exposant est la caractéristique du logarithme et la partie significative est proche de sa mantisse.
IEEE 754
La norme IEEE 754 définit des formats de flottants binaires (donc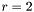 ) et impose aussi des contraintes de précision sur les calculs effectués. Il y a 3 formats utilisés en pratique: simple, double et étendu, ce dernier étant moins souvent présent et parfois pas utilisé même quand il est supporté par le hardware. Le format simple est utilisé pour les float, le double pour les double et le format étendu pour les long double.
) et impose aussi des contraintes de précision sur les calculs effectués. Il y a 3 formats utilisés en pratique: simple, double et étendu, ce dernier étant moins souvent présent et parfois pas utilisé même quand il est supporté par le hardware. Le format simple est utilisé pour les float, le double pour les double et le format étendu pour les long double.
Tous ces formats ont aussi une représentation pour 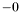 ,
, 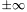 et des NaN.
et des NaN.
A noter que la norme ne définit pas de représentation pour ces formats.
Valeurs
A titre d'exemple, voici un tableau regroupant les valeurs minimales demandées par la norme C ainsi que les caractéristiques des formats IEEE 754.
| float C | double C | IEEE simple | IEEE double | IEEE étendu
| |
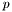 | 24 | 53 | 64
| ||
| DIG | 6 | 10 | 6 | 15 | 18
|
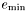 | -125 | -1021 | -16381
| ||
| MIN_10_EXP | -37 | -37 | -37 | -307 | -4931
|
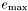 | 128 | 1024 | 16384
| ||
| MAX_10_EXP | 37 | 37 | 38 | 308 | 4932
|
| MAX | 1E37 | 1E37 | 3.40E38 | 1.80E308 | 1.19E4932
|
| EPSILON | 1E-5 | 1E-9 | 1.19E-7 | 2.22E-16 | 1.08E-19
|
| MIN | 1E-37 | 1E-37 | 1.18E-38 | 2.23E-308 | 3.36E-4932
|
DIG
DIG est déterminé par la formule:
![\[ \left\{\begin{array}{ll} \lfloor (p-1) \; \log_{10} r\rfloor + 1 & \mbox{si $r$ est une puissance de 10} \\ \lfloor (p-1) \; \log_{10} r\rfloor & \mbox{sinon} \end{array}\right. \]](form_59.png)
Le cas général est une borne inférieure qui est atteinte si l'intervalle des exposants est suffisemment grand. Il s'obtient en remarquant que pour être sûr qu'il n'y a pas de perte dans la conversion décimal en autre base, il faut qu'à tout endroit, l'intervalle entre deux flottants de base 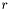 soit inférieur à l'intervalle entre deux flottants décimaux de précision
soit inférieur à l'intervalle entre deux flottants décimaux de précision 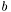 . Le premier vaut au maximum
. Le premier vaut au maximum 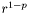 . Le dernier vaut au minimum
. Le dernier vaut au minimum 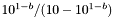 . On va négliger le terme
. On va négliger le terme 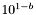 au dénominateur. On a donc:
au dénominateur. On a donc:
![\[\begin{array}{lll} r^{1-p} & \leq & \frac{10^{1-b}}{10}\\ \log_{10} r^{1-p} & \leq & \log_{10} 10^{1-b} - \log_{10} 10\\ (1-p) \log_{10} r & \leq & (1-b)\log_{10} 10 - 1\\ (1-p) \log_{10} r & \leq & 1-b-1\\ b & \leq & (p-1) \log_{10} r \\ \end{array}\]](form_69.png)
Le 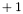 du cas où
du cas où 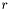 est une puissance de 10 provient du fait que dans ce cas il y a une corrélation entre les minimums et maximums de l'intervalle entre deux flottants entre le cas décimal et le cas base
est une puissance de 10 provient du fait que dans ce cas il y a une corrélation entre les minimums et maximums de l'intervalle entre deux flottants entre le cas décimal et le cas base 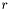 .
.
Dans le cas des formats IEEE, les formats simples et étendus sont affectés par l'utilisation de 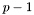 plutôt que d'un
plutôt que d'un 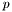 qui aurait mieux correspondu à l'intuition. Dans le cas du format simple, cette bonne inférieure est atteinte, par exemple 9.9999994e-04 ce trouve entre ces deux flottants:
qui aurait mieux correspondu à l'intuition. Dans le cas du format simple, cette bonne inférieure est atteinte, par exemple 9.9999994e-04 ce trouve entre ces deux flottants:
0x1.0624d2p-10 = 9.999993e-04 = 9.99999349e-04
0x1.0624d4p-10 = 9.999995e-04 = 9.99999465e-04
De même pour le format extended, 9.999999999999999998e-04 se trouve entre ces flottants:
0x8.3126e978d4fdf39p-13 = 9.999999999999999997e-04 = 9.99999999999999999747e-04
0x8.3126e978d4fdf3ap-13 = 9.999999999999999999e-04 = 9.99999999999999999853e-04
(le format double a 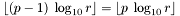 ).
).